개발자라면 다들 파이썬에서 random 모듈을 사용하여 난수를 생성해본 적이 있을 것이다.
random 모듈에는 random(), randint(a, b) 와 같은 다양한 내장함수들이 제공되어 이를 활용한 난수 생성이 가능
이전 글 참고 : https://sallysooo.tistory.com/41
[Python] 파이썬 random 모듈 내장 함수 정리
1. random.random()- 0.0 이상 1.0 미만의 부동 소수점 난수를 반환import random# 0.0 이상 1.0 미만의 난수 생성result = random.random()print("random.random():", result) 2. random.randint(a, b)- a 이상 b 이하의 정수 난수를
sallysooo.tistory.com
이렇게 random 모듈의 사용법은 알지만, 문득 random 모듈 자체가 무슨 원리로 난수를 생성하는지 궁금해졌다..
결론부터 말하자면 파이썬은 메르센 트위스터 (mersenne twister)를 이용하여 난수를 생성한다.
아래에서 더 자세히 알아보자!
메르센 트위스터?
- 컴퓨터에서 난수를 생성하는 데 사용하는 알고리즘 중 하나
- 파이썬의 random 모듈이 사용하는 기본 난수 생성기가 바로 이 메르센 트위스터이며, 파이썬뿐만 아니라 C++, excel, matlab 등에서 의사 난수 생성기로 사용하고 있음
- 메르센 소수를 이용해 만들어짐
(* 메르센 수 : 2의 거듭제곱에서 1이 모자란 숫자)
(* 메르센 소수: 메르센 수 중에 소수인 숫자들)
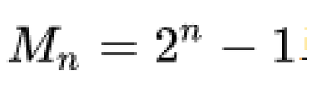
- 이런 메르센 소수와 비트 연산을 활용해 난수를 생성하는 것이 메르센 트위스터 알고리즘
- LFSR (Linear Feedback Shift Register) 계열의 의사 난수 생성기로, 선형 연산인 XOR 연산을 통해 다음 상태를 생성
+ ) 난수 생성기?
컴퓨터는 사실 진짜 "무작위"한 숫자를 만들어내는 데에는 한계가 있다.
대신 "의사 난수 생성기" (pseudo-random number generator)라는 걸 사용해 일정한 규칙에 따라 무작위처럼 보이는 숫자들을 만들어낸다.
이 규칙이 복잡해서, 결과적으로 나오는 숫자들이 예측할 수 없게 만들어져야 함
메르센 트위스터의 특징
- 긴 주기
- 메르센 트위스터는 매우 긴 주기를 가짐
- 주기란 "난수"가 반복되기 전까지 생성되는 숫자들의 길이를 말하는데, 메르센 의 경우 그 주기가 2^19937-1
(약 10 ^ 6001) 이다.
- 이는 엄청나게 긴 숫자열이므로 사실상 중복된 패턴이 나올 일이 거의 없음 - 빠르고 효율적
- 매우 빠른 속도로 숫자를 생성하여 많은 프로그래밍 언어와 소프트웨어에서 기본 난수 생성기로 채택하고 있음 - 균일한 분포
- 메르센 트위스터가 생성하는 난수는 특정 패턴을 따르지 않고, 전체적으로 고르게 분포된다는 특징
- 이는 시뮬레이션, 게임, 암호화 등 다양한 응용 분야에서 중요한 특성
메르센 트위스터가 중요한 이유
- 파이썬의 random 모듈에서 random.random(), random.randint() 등 다양한 함수가 사용하는 기본 알고리즘이 메르센 트위스터이다. 즉, 파이썬에서 난수를 생성할 때 이 알고리즘의 특성을 이해하는 것이 중요하다.
- 이 알고리즘 덕에 파이썬은 신뢰할 수 있고, 예측하기 어려운 숫자들을 빠르게 생성할 수 있음
또한 파이썬의 random 모듈의 소스코드는 C언어로 작성되어 최적화 되어있음
- 단, 예측이 가능할 수도 있기 때문에 보안이 중요한 암호화 용도로는 적합하지 않아 secret 모듈을 사용하거나 random.SystemRandom()와 같은 좀 더 강력한 방법을 사용하는 것이 좋음
메르센 트위스터 알고리즘 (C++)
/* Period parameters -- These are all magic. Don't change. */
#define N 624
#define M 397
#define MATRIX_A 0x9908b0dfU /* constant vector a */
#define UPPER_MASK 0x80000000U /* most significant w-r bits */
#define LOWER_MASK 0x7fffffffU /* least significant r bits */
static uint32_t
genrand_uint32(RandomObject *self)
{
uint32_t y;
static const uint32_t mag01[2] = {0x0U, MATRIX_A};
/* mag01[x] = x * MATRIX_A for x=0,1 */
uint32_t *mt;
mt = self->state;
if (self->index >= N) { /* generate N words at one time */
int kk;
for (kk=0;kk<N-M;kk++) {
y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1U];
}
for (;kk<N-1;kk++) {
y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
mt[kk] = mt[kk+(M-N)] ^ (y >> 1) ^ mag01[y & 0x1U];
}
y = (mt[N-1]&UPPER_MASK)|(mt[0]&LOWER_MASK);
mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1U];
self->index = 0;
}
y = mt[self->index++];
y ^= (y >> 11);
y ^= (y << 7) & 0x9d2c5680U;
y ^= (y << 15) & 0xefc60000U;
y ^= (y >> 18);
return y;
}
위 코드는 genrand_uint32 라는 함수로, 32비트의 무작위 숫자 하나를 생성하여 반환한다.
이 함수는 메르센 트위스터의 내부 상태를 업데이트하며, self라는 객체에 있는 배열을 사용해 난수를 생성함
뜯어서 분석해보자.
(아래에서 말하는 '상태 배열'이란 state array를 직역한 것)
/* Period parameters -- These are all magic. Don't change. */
#define N 624
#define M 397
#define MATRIX_A 0x9908b0dfU /* constant vector a */
#define UPPER_MASK 0x80000000U /* most significant w-r bits */
#define LOWER_MASK 0x7fffffffU /* least significant r bits */- N과 M은 메르센 트위스터에서 사용하는 기본 매개변수
- N은 상태 배열의 크기(624)이고, M은 중간 단계에서 사용하는 인덱스 오프셋 (397)
- MATRIX_A는 난수 생성에 필요한 고정된 상수 (constant vector)
- UPPER_MASK와 LOWER_MASK는 상태 배열에서 상위 및 하위 비트를 구분하는 데 사용되는 마스크 (mask)
static uint32_t
genrand_uint32(RandomObject *self)
{
uint32_t y;
static const uint32_t mag01[2] = {0x0U, MATRIX_A};- RandomObject 라는 구조체를 받아 32비트의 무작위 숫자를 반환하는 genrand_unit32 함수
- y라는 32비트 정수를 선언
- mag01 배열은 두 개의 값 (0과 MATRIX_A)을 가지며, 이 배열은 이후 XOR 연산을 통해 난수를 섞는 데에 사용
uint32_t *mt;
mt = self->state;
if (self->index >= N) { /* generate N words at one time */
int kk;
for (kk=0; kk<N-M; kk++) {
y = (mt[kk] & UPPER_MASK) | (mt[kk+1] & LOWER_MASK);
mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1U];
}- mt => 메르센 트위스터의 상태 배열을 가리키는 포인터로, 해당 배열에는 난수 생성에 필요한 내부 상태가 저장됨
- 조건문을 통해 상태 배열이 다 사용되었는지를 확인한다. 만약 다 사용되었다면, 새로운 N개의 숫자를 생성해 배열을 다시 채움
- for 루프는 상태 배열의 앞부분을 업데이트함
- UPPER_MASK 와 LOWER_MASK를 사용해 상위와 하위 비트를 조합한 후, y를 오른쪽으로 shift 하고 mag01 값을 XOR 연산으로 섞음
for (; kk<N-1; kk++) {
y = (mt[kk] & UPPER_MASK) | (mt[kk+1] & LOWER_MASK);
mt[kk] = mt[kk+(M-N)] ^ (y >> 1) ^ mag01[y & 0x1U];
}
y = (mt[N-1] & UPPER_MASK) | (mt[0] & LOWER_MASK);
mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1U];
self->index = 0;
}- 두 번째 for 루프는 나머지 상태 배열을 업데이트
- 마지막으로 상태 배열의 마지막 요소를 업데이트하며, 이때 배열의 첫 번째 요소를 사용하여 계산
- 상태 배열이 새로 갱신되었으므로, 인덱스를 0으로 리셋
y = mt[self->index++];
y ^= (y >> 11);
y ^= (y << 7) & 0x9d2c5680U;
y ^= (y << 15) & 0xefc60000U;
y ^= (y >> 18);
return y;- 현재 인덱스의 상태 배열 값을 가져와 y에 저장하고, 인덱스를 하나 증가시킴
- 그 후 최종 난수를 얻기 위해 여러 번의 XOR 연산을 수행하는 단계를 거쳐서 난수의 분포를 더 무작위화
- 마지막으로, 생성된 난수 y를 반환
메르센 트위스터 알고리즘 (Python)
class MersenneTwister:
def __init__(self, seed):
self.N = 624
self.M = 397
self.MATRIX_A = 0x9908b0df
self.UPPER_MASK = 0x80000000
self.LOWER_MASK = 0x7fffffff
# Initialize the state vector with the seed
self.mt = [0] * self.N
self.mt[0] = seed
for i in range(1, self.N):
self.mt[i] = 0xffffffff & (1812433253 * (self.mt[i-1] ^ (self.mt[i-1] >> 30)) + i)
self.index = self.N
def generate_numbers(self):
for i in range(self.N):
y = (self.mt[i] & self.UPPER_MASK) | (self.mt[(i+1) % self.N] & self.LOWER_MASK)
self.mt[i] = self.mt[(i + self.M) % self.N] ^ (y >> 1)
if y % 2 != 0:
self.mt[i] ^= self.MATRIX_A
def random_int(self):
if self.index >= self.N:
self.generate_numbers()
self.index = 0
y = self.mt[self.index]
self.index += 1
# Tempering
y ^= (y >> 11)
y ^= (y << 7) & 0x9d2c5680
y ^= (y << 15) & 0xefc60000
y ^= (y >> 18)
return y
# Example usage:
mt = MersenneTwister(5489) # Seed value
print(mt.random_int())
기존의 메르센 트위스터 알고리즘은 앞선 코드와 같이 C++로 작성된 것이었으나...
위의 C++ 문법을 파이썬으로 바꾼 코드로 다시 분석해보자.
기본적으로 내부 상태 배열을 사용하여 난수를 생성하고, 이 상태 배열을 계속 갱신하면서 새로운 난수를 만드는 방식!
class MersenneTwister:
def __init__(self, seed):
self.N = 624
self.M = 397
self.MATRIX_A = 0x9908b0df
self.UPPER_MASK = 0x80000000
self.LOWER_MASK = 0x7fffffff
# Initialize the state vector with the seed
self.mt = [0] * self.N # 난수 생성을 위한 내부 상태를 저장
self.mt[0] = seed # seed 입력값이 상태 배열의 첫 번째 요소
for i in range(1, self.N):
self.mt[i] = 0xffffffff & (1812433253 * (self.mt[i-1] ^ (self.mt[i-1] >> 30)) + i)
self.index = self.N- init 초기화 메소드에는 seed 초기값을 받아 난수 생성을 위한 상태를 설정
- N은 상태 배열의 크기(624), M은 상태 배열의 특정 부분을 참조할 때 사용하는 오프셋(397)로 고정된 상수 설정
- MATRIX_A 는 난수 생성에 사용되는 고정된 상수
- UPPER_MASK, LOWER_MASK 는 상위 비트와 하위 비트를 분리하는데 사용되는 마스크로, 비트 연산을 통해 상태를 섞을 때 활용됨
- for 루프에서는 상태 배열 mt의 나머지 요소들을 초기화한다. 이전 요소인 self.mt [i-1]을 기반으로 새 요소를 계산하며, 비트 연산과 곱셈을 통해 값을 생성함
- self.index는 상태 배열에서 현재 위치를 가리키며, 초기값으로 N을 설정해 배열이 다 소진되었음을 나타냄
def generate_numbers(self):
for i in range(self.N):
y = (self.mt[i] & self.UPPER_MASK) | (self.mt[(i+1) % self.N] & self.LOWER_MASK)
self.mt[i] = self.mt[(i + self.M) % self.N] ^ (y >> 1)
if y % 2 != 0:
self.mt[i] ^= self.MATRIX_A- 상태 배열을 갱신하여 새로운 난수를 생성하는 역할을 하는 함수로, 상태 배열이 모두 사용되었을 때 호출됨
- 상태 섞기 : 상태 배열의 각 요소에 대해 상위비트와 하위비트를 OR 연산자(|)로 결합하여 y를 만듦
- 상태 갱신 : y의 오른쪽 시프트(>>1) 연산 후, 결과를 XOR 연산으로 섞어 상태 배열의 새로운 값을 만듦
- 짝수/홀수 처리 : y가 홀수일 경우 (y % 2 != 0) MATRIX_A를 추가로 XOR 연산하여 값을 더 섞음
def random_int(self):
if self.index >= self.N:
self.generate_numbers()
self.index = 0
y = self.mt[self.index]
self.index += 1
# Tempering
y ^= (y >> 11)
y ^= (y << 7) & 0x9d2c5680
y ^= (y << 15) & 0xefc60000
y ^= (y >> 18)
return y
# Example usage:
mt = MersenneTwister(5489) # Seed value
print(mt.random_int())- 상태 배열에서 난수를 가져오려 할 때, index가 N보다 크면 상태 배열이 다 사용되었음을 의미하므로, 앞서 설명한 generate_numbers() 함수로 새로운 숫자들을 생성
- 새로운 난수로 세팅된 mt 배열에 대하여 현재 index의 상태 배열 값을 y에 저장하고 1 증가
- 이후 네 번의 XOR 연산으로 값을 뒤섞어 더 균일한 난수를 만들어내어 최종 난수 값을 더 무작위화함 (템퍼링)
- 최종적으로 생성된 난수 y를 반환한다.
즉 위 메르센 트위스터 알고리즘의 단계를 요약해보자면 다음과 같다!
- 상태 배열 초기화 : seed 값을 바탕으로 상태 배열을 생성
- 상태 갱신 : 상태 배열의 값을 갱신해 새로운 난수 시퀀스를 준비
- 난수 생성 및 템퍼링 : 상태 배열에서 값을 꺼내고, 여러 비트 연산으로 값을 섞어 최종 난수를 반환
'Cryptography' 카테고리의 다른 글
| [Crypto] 암호학 기본 개념 및 SSH 이해하기 - 대칭키(AES), 비대칭키(RSA) 알고리즘 (0) | 2024.11.28 |
|---|---|
| [Crypto] Double DES 문제 풀이 (0) | 2024.08.31 |
| [Crypto] 고전 암호와 현대 암호 알아보기 (1) | 2024.08.30 |
| [Crypto] 메르센 트위스터의 난수 생성 예측하기 (0) | 2024.08.28 |
| [Crypto] 암호학 툴 설치하기 (0) | 2024.08.27 |
개발자라면 다들 파이썬에서 random 모듈을 사용하여 난수를 생성해본 적이 있을 것이다.
random 모듈에는 random(), randint(a, b) 와 같은 다양한 내장함수들이 제공되어 이를 활용한 난수 생성이 가능
이전 글 참고 : https://sallysooo.tistory.com/41
[Python] 파이썬 random 모듈 내장 함수 정리
1. random.random()- 0.0 이상 1.0 미만의 부동 소수점 난수를 반환import random# 0.0 이상 1.0 미만의 난수 생성result = random.random()print("random.random():", result) 2. random.randint(a, b)- a 이상 b 이하의 정수 난수를
sallysooo.tistory.com
이렇게 random 모듈의 사용법은 알지만, 문득 random 모듈 자체가 무슨 원리로 난수를 생성하는지 궁금해졌다..
결론부터 말하자면 파이썬은 메르센 트위스터 (mersenne twister)를 이용하여 난수를 생성한다.
아래에서 더 자세히 알아보자!
메르센 트위스터?
- 컴퓨터에서 난수를 생성하는 데 사용하는 알고리즘 중 하나
- 파이썬의 random 모듈이 사용하는 기본 난수 생성기가 바로 이 메르센 트위스터이며, 파이썬뿐만 아니라 C++, excel, matlab 등에서 의사 난수 생성기로 사용하고 있음
- 메르센 소수를 이용해 만들어짐
(* 메르센 수 : 2의 거듭제곱에서 1이 모자란 숫자)
(* 메르센 소수: 메르센 수 중에 소수인 숫자들)
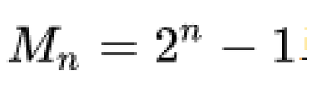
- 이런 메르센 소수와 비트 연산을 활용해 난수를 생성하는 것이 메르센 트위스터 알고리즘
- LFSR (Linear Feedback Shift Register) 계열의 의사 난수 생성기로, 선형 연산인 XOR 연산을 통해 다음 상태를 생성
+ ) 난수 생성기?
컴퓨터는 사실 진짜 "무작위"한 숫자를 만들어내는 데에는 한계가 있다.
대신 "의사 난수 생성기" (pseudo-random number generator)라는 걸 사용해 일정한 규칙에 따라 무작위처럼 보이는 숫자들을 만들어낸다.
이 규칙이 복잡해서, 결과적으로 나오는 숫자들이 예측할 수 없게 만들어져야 함
메르센 트위스터의 특징
- 긴 주기
- 메르센 트위스터는 매우 긴 주기를 가짐
- 주기란 "난수"가 반복되기 전까지 생성되는 숫자들의 길이를 말하는데, 메르센 의 경우 그 주기가 2^19937-1
(약 10 ^ 6001) 이다.
- 이는 엄청나게 긴 숫자열이므로 사실상 중복된 패턴이 나올 일이 거의 없음 - 빠르고 효율적
- 매우 빠른 속도로 숫자를 생성하여 많은 프로그래밍 언어와 소프트웨어에서 기본 난수 생성기로 채택하고 있음 - 균일한 분포
- 메르센 트위스터가 생성하는 난수는 특정 패턴을 따르지 않고, 전체적으로 고르게 분포된다는 특징
- 이는 시뮬레이션, 게임, 암호화 등 다양한 응용 분야에서 중요한 특성
메르센 트위스터가 중요한 이유
- 파이썬의 random 모듈에서 random.random(), random.randint() 등 다양한 함수가 사용하는 기본 알고리즘이 메르센 트위스터이다. 즉, 파이썬에서 난수를 생성할 때 이 알고리즘의 특성을 이해하는 것이 중요하다.
- 이 알고리즘 덕에 파이썬은 신뢰할 수 있고, 예측하기 어려운 숫자들을 빠르게 생성할 수 있음
또한 파이썬의 random 모듈의 소스코드는 C언어로 작성되어 최적화 되어있음
- 단, 예측이 가능할 수도 있기 때문에 보안이 중요한 암호화 용도로는 적합하지 않아 secret 모듈을 사용하거나 random.SystemRandom()와 같은 좀 더 강력한 방법을 사용하는 것이 좋음
메르센 트위스터 알고리즘 (C++)
/* Period parameters -- These are all magic. Don't change. */
#define N 624
#define M 397
#define MATRIX_A 0x9908b0dfU /* constant vector a */
#define UPPER_MASK 0x80000000U /* most significant w-r bits */
#define LOWER_MASK 0x7fffffffU /* least significant r bits */
static uint32_t
genrand_uint32(RandomObject *self)
{
uint32_t y;
static const uint32_t mag01[2] = {0x0U, MATRIX_A};
/* mag01[x] = x * MATRIX_A for x=0,1 */
uint32_t *mt;
mt = self->state;
if (self->index >= N) { /* generate N words at one time */
int kk;
for (kk=0;kk<N-M;kk++) {
y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1U];
}
for (;kk<N-1;kk++) {
y = (mt[kk]&UPPER_MASK)|(mt[kk+1]&LOWER_MASK);
mt[kk] = mt[kk+(M-N)] ^ (y >> 1) ^ mag01[y & 0x1U];
}
y = (mt[N-1]&UPPER_MASK)|(mt[0]&LOWER_MASK);
mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1U];
self->index = 0;
}
y = mt[self->index++];
y ^= (y >> 11);
y ^= (y << 7) & 0x9d2c5680U;
y ^= (y << 15) & 0xefc60000U;
y ^= (y >> 18);
return y;
}
위 코드는 genrand_uint32 라는 함수로, 32비트의 무작위 숫자 하나를 생성하여 반환한다.
이 함수는 메르센 트위스터의 내부 상태를 업데이트하며, self라는 객체에 있는 배열을 사용해 난수를 생성함
뜯어서 분석해보자.
(아래에서 말하는 '상태 배열'이란 state array를 직역한 것)
/* Period parameters -- These are all magic. Don't change. */
#define N 624
#define M 397
#define MATRIX_A 0x9908b0dfU /* constant vector a */
#define UPPER_MASK 0x80000000U /* most significant w-r bits */
#define LOWER_MASK 0x7fffffffU /* least significant r bits */- N과 M은 메르센 트위스터에서 사용하는 기본 매개변수
- N은 상태 배열의 크기(624)이고, M은 중간 단계에서 사용하는 인덱스 오프셋 (397)
- MATRIX_A는 난수 생성에 필요한 고정된 상수 (constant vector)
- UPPER_MASK와 LOWER_MASK는 상태 배열에서 상위 및 하위 비트를 구분하는 데 사용되는 마스크 (mask)
static uint32_t
genrand_uint32(RandomObject *self)
{
uint32_t y;
static const uint32_t mag01[2] = {0x0U, MATRIX_A};- RandomObject 라는 구조체를 받아 32비트의 무작위 숫자를 반환하는 genrand_unit32 함수
- y라는 32비트 정수를 선언
- mag01 배열은 두 개의 값 (0과 MATRIX_A)을 가지며, 이 배열은 이후 XOR 연산을 통해 난수를 섞는 데에 사용
uint32_t *mt;
mt = self->state;
if (self->index >= N) { /* generate N words at one time */
int kk;
for (kk=0; kk<N-M; kk++) {
y = (mt[kk] & UPPER_MASK) | (mt[kk+1] & LOWER_MASK);
mt[kk] = mt[kk+M] ^ (y >> 1) ^ mag01[y & 0x1U];
}- mt => 메르센 트위스터의 상태 배열을 가리키는 포인터로, 해당 배열에는 난수 생성에 필요한 내부 상태가 저장됨
- 조건문을 통해 상태 배열이 다 사용되었는지를 확인한다. 만약 다 사용되었다면, 새로운 N개의 숫자를 생성해 배열을 다시 채움
- for 루프는 상태 배열의 앞부분을 업데이트함
- UPPER_MASK 와 LOWER_MASK를 사용해 상위와 하위 비트를 조합한 후, y를 오른쪽으로 shift 하고 mag01 값을 XOR 연산으로 섞음
for (; kk<N-1; kk++) {
y = (mt[kk] & UPPER_MASK) | (mt[kk+1] & LOWER_MASK);
mt[kk] = mt[kk+(M-N)] ^ (y >> 1) ^ mag01[y & 0x1U];
}
y = (mt[N-1] & UPPER_MASK) | (mt[0] & LOWER_MASK);
mt[N-1] = mt[M-1] ^ (y >> 1) ^ mag01[y & 0x1U];
self->index = 0;
}- 두 번째 for 루프는 나머지 상태 배열을 업데이트
- 마지막으로 상태 배열의 마지막 요소를 업데이트하며, 이때 배열의 첫 번째 요소를 사용하여 계산
- 상태 배열이 새로 갱신되었으므로, 인덱스를 0으로 리셋
y = mt[self->index++];
y ^= (y >> 11);
y ^= (y << 7) & 0x9d2c5680U;
y ^= (y << 15) & 0xefc60000U;
y ^= (y >> 18);
return y;- 현재 인덱스의 상태 배열 값을 가져와 y에 저장하고, 인덱스를 하나 증가시킴
- 그 후 최종 난수를 얻기 위해 여러 번의 XOR 연산을 수행하는 단계를 거쳐서 난수의 분포를 더 무작위화
- 마지막으로, 생성된 난수 y를 반환
메르센 트위스터 알고리즘 (Python)
class MersenneTwister:
def __init__(self, seed):
self.N = 624
self.M = 397
self.MATRIX_A = 0x9908b0df
self.UPPER_MASK = 0x80000000
self.LOWER_MASK = 0x7fffffff
# Initialize the state vector with the seed
self.mt = [0] * self.N
self.mt[0] = seed
for i in range(1, self.N):
self.mt[i] = 0xffffffff & (1812433253 * (self.mt[i-1] ^ (self.mt[i-1] >> 30)) + i)
self.index = self.N
def generate_numbers(self):
for i in range(self.N):
y = (self.mt[i] & self.UPPER_MASK) | (self.mt[(i+1) % self.N] & self.LOWER_MASK)
self.mt[i] = self.mt[(i + self.M) % self.N] ^ (y >> 1)
if y % 2 != 0:
self.mt[i] ^= self.MATRIX_A
def random_int(self):
if self.index >= self.N:
self.generate_numbers()
self.index = 0
y = self.mt[self.index]
self.index += 1
# Tempering
y ^= (y >> 11)
y ^= (y << 7) & 0x9d2c5680
y ^= (y << 15) & 0xefc60000
y ^= (y >> 18)
return y
# Example usage:
mt = MersenneTwister(5489) # Seed value
print(mt.random_int())
기존의 메르센 트위스터 알고리즘은 앞선 코드와 같이 C++로 작성된 것이었으나...
위의 C++ 문법을 파이썬으로 바꾼 코드로 다시 분석해보자.
기본적으로 내부 상태 배열을 사용하여 난수를 생성하고, 이 상태 배열을 계속 갱신하면서 새로운 난수를 만드는 방식!
class MersenneTwister:
def __init__(self, seed):
self.N = 624
self.M = 397
self.MATRIX_A = 0x9908b0df
self.UPPER_MASK = 0x80000000
self.LOWER_MASK = 0x7fffffff
# Initialize the state vector with the seed
self.mt = [0] * self.N # 난수 생성을 위한 내부 상태를 저장
self.mt[0] = seed # seed 입력값이 상태 배열의 첫 번째 요소
for i in range(1, self.N):
self.mt[i] = 0xffffffff & (1812433253 * (self.mt[i-1] ^ (self.mt[i-1] >> 30)) + i)
self.index = self.N- init 초기화 메소드에는 seed 초기값을 받아 난수 생성을 위한 상태를 설정
- N은 상태 배열의 크기(624), M은 상태 배열의 특정 부분을 참조할 때 사용하는 오프셋(397)로 고정된 상수 설정
- MATRIX_A 는 난수 생성에 사용되는 고정된 상수
- UPPER_MASK, LOWER_MASK 는 상위 비트와 하위 비트를 분리하는데 사용되는 마스크로, 비트 연산을 통해 상태를 섞을 때 활용됨
- for 루프에서는 상태 배열 mt의 나머지 요소들을 초기화한다. 이전 요소인 self.mt [i-1]을 기반으로 새 요소를 계산하며, 비트 연산과 곱셈을 통해 값을 생성함
- self.index는 상태 배열에서 현재 위치를 가리키며, 초기값으로 N을 설정해 배열이 다 소진되었음을 나타냄
def generate_numbers(self):
for i in range(self.N):
y = (self.mt[i] & self.UPPER_MASK) | (self.mt[(i+1) % self.N] & self.LOWER_MASK)
self.mt[i] = self.mt[(i + self.M) % self.N] ^ (y >> 1)
if y % 2 != 0:
self.mt[i] ^= self.MATRIX_A- 상태 배열을 갱신하여 새로운 난수를 생성하는 역할을 하는 함수로, 상태 배열이 모두 사용되었을 때 호출됨
- 상태 섞기 : 상태 배열의 각 요소에 대해 상위비트와 하위비트를 OR 연산자(|)로 결합하여 y를 만듦
- 상태 갱신 : y의 오른쪽 시프트(>>1) 연산 후, 결과를 XOR 연산으로 섞어 상태 배열의 새로운 값을 만듦
- 짝수/홀수 처리 : y가 홀수일 경우 (y % 2 != 0) MATRIX_A를 추가로 XOR 연산하여 값을 더 섞음
def random_int(self):
if self.index >= self.N:
self.generate_numbers()
self.index = 0
y = self.mt[self.index]
self.index += 1
# Tempering
y ^= (y >> 11)
y ^= (y << 7) & 0x9d2c5680
y ^= (y << 15) & 0xefc60000
y ^= (y >> 18)
return y
# Example usage:
mt = MersenneTwister(5489) # Seed value
print(mt.random_int())- 상태 배열에서 난수를 가져오려 할 때, index가 N보다 크면 상태 배열이 다 사용되었음을 의미하므로, 앞서 설명한 generate_numbers() 함수로 새로운 숫자들을 생성
- 새로운 난수로 세팅된 mt 배열에 대하여 현재 index의 상태 배열 값을 y에 저장하고 1 증가
- 이후 네 번의 XOR 연산으로 값을 뒤섞어 더 균일한 난수를 만들어내어 최종 난수 값을 더 무작위화함 (템퍼링)
- 최종적으로 생성된 난수 y를 반환한다.
즉 위 메르센 트위스터 알고리즘의 단계를 요약해보자면 다음과 같다!
- 상태 배열 초기화 : seed 값을 바탕으로 상태 배열을 생성
- 상태 갱신 : 상태 배열의 값을 갱신해 새로운 난수 시퀀스를 준비
- 난수 생성 및 템퍼링 : 상태 배열에서 값을 꺼내고, 여러 비트 연산으로 값을 섞어 최종 난수를 반환
'Cryptography' 카테고리의 다른 글
| [Crypto] 암호학 기본 개념 및 SSH 이해하기 - 대칭키(AES), 비대칭키(RSA) 알고리즘 (0) | 2024.11.28 |
|---|---|
| [Crypto] Double DES 문제 풀이 (0) | 2024.08.31 |
| [Crypto] 고전 암호와 현대 암호 알아보기 (1) | 2024.08.30 |
| [Crypto] 메르센 트위스터의 난수 생성 예측하기 (0) | 2024.08.28 |
| [Crypto] 암호학 툴 설치하기 (0) | 2024.08.27 |
