메르센 트위스터는 널리 사용되는 의사 난수 생성기(PRNG)이다.
이 PRNG는 32bit 정수를 생성하고, 내부적으로는 624개의 상태를 유지하며 이 상태를 기반으로 새로운 난수를 생성한다.
이 PRNG의 특징은 높은 주기 (2^19937-1)와 좋은 통계적 성질을 가진다.
그러나 624개의 연속된 출력을 보면 다음 출력을 정확하게 예측할 수 있게 된다는 특징이 있다.
따라서 이를 바탕으로 작성된 아래의 프로그램은 624개의 연속된 출력을 관찰하고, 그 이후의 출력을 예측한다.
중요한 점은 초기 seed나 시작 위치에 관계없이 작동한다는 것!
프로그램은 입력된 숫자들을 디코딩하여 내부 상태를 복구한 후, 그 상태를 바탕으로 이후의 출력을 예측한다.
https://gist.github.com/Rhomboid/b1a882c70b7a1901efa9
Predict output of Mersenne Twister after seeing 624 values
Predict output of Mersenne Twister after seeing 624 values - mersenne_predict.py
gist.github.com
먼저 위 깃헙의 메르센 트위스터 예측 코드를 한 번 분석해보고자 한다.
- 전체 코드
#!/usr/bin/env python
#
# Mersenne Twister predictor
#
# Feed this program the output of any 32-bit MT19937 Mersenne Twister and
# after seeing 624 values it will correctly predict the rest.
#
# The values may come from any point in the sequence -- the program does not
# need to see the first 624 values, just *any* 624 consecutive values. The
# seed used is also irrelevant, and it will work even if the generator was
# seeded from /dev/random or any other high quality source.
#
# The values should be in decimal, one per line, on standard input.
#
# The program expects the actual unsigned 32 bit integer values taken directly
# from the output of the Mersenne Twister. It won't work if they've been
# scaled or otherwise modified, such as by using modulo or
# std::uniform_int_distribution to alter the distribution/range. In principle
# it would be possible to cope with such a scenario if you knew the exact
# parameters used by such an algorithm, but this program does not have any
# such knowledge.
#
# For more information, refer to the original 1998 paper:
#
# "Mersenne Twister: A 623-dimensionally equidistributed uniform pseudorandom
# number generator", Makoto Matsumoto, Takuji Nishimura, 1998
#
# http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.215.1141
#
# This code is not written with speed or efficiency in mind, but to follow
# as closely as possible to the terminology and naming in the paper.
#
# License: CC0 http://creativecommons.org/publicdomain/zero/1.0/
from __future__ import print_function
import sys
import collections
class Params:
# clearly a mathematician and not a programmer came up with these names
# because a dozen single-letter names would ordinarily be insane
w = 32 # word size
n = 624 # degree of recursion
m = 397 # middle term
r = 31 # separation point of one word
a = 0x9908b0df # bottom row of matrix A
u = 11 # tempering shift
s = 7 # tempering shift
t = 15 # tempering shift
l = 18 # tempering shift
b = 0x9d2c5680 # tempering mask
c = 0xefc60000 # tempering mask
def undo_xor_rshift(x, shift):
''' reverses the operation x ^= (x >> shift) '''
result = x
for shift_amount in range(shift, Params.w, shift):
result ^= (x >> shift_amount)
return result
def undo_xor_lshiftmask(x, shift, mask):
''' reverses the operation x ^= ((x << shift) & mask) '''
window = (1 << shift) - 1
for _ in range(Params.w // shift):
x ^= (((window & x) << shift) & mask)
window <<= shift
return x
def temper(x):
''' tempers the value to improve k-distribution properties '''
x ^= (x >> Params.u)
x ^= ((x << Params.s) & Params.b)
x ^= ((x << Params.t) & Params.c)
x ^= (x >> Params.l)
return x
def untemper(x):
''' reverses the tempering operation '''
x = undo_xor_rshift(x, Params.l)
x = undo_xor_lshiftmask(x, Params.t, Params.c)
x = undo_xor_lshiftmask(x, Params.s, Params.b)
x = undo_xor_rshift(x, Params.u)
return x
def upper(x):
''' return the upper (w - r) bits of x '''
return x & ((1 << Params.w) - (1 << Params.r))
def lower(x):
''' return the lower r bits of x '''
return x & ((1 << Params.r) - 1)
def timesA(x):
''' performs the equivalent of x*A '''
if x & 1:
return (x >> 1) ^ Params.a
else:
return (x >> 1)
seen = collections.deque(maxlen=Params.n)
print('waiting for {} previous inputs'.format(Params.n))
for _ in range(Params.n):
val = untemper(int(sys.stdin.readline()))
seen.append(val)
num_correct = num_incorrect = 0
print('ready to predict')
while True:
# The recurrence relation is:
#
# x[k + n] = x[k + m] ^ timesA(upper(x[k]) | lower(x[k + 1]))
#
# Substituting j = k + n gives
#
# x[j] = x[j - n + m] ^ timesA(upper(x[j - n]) | lower(x[j - n + 1]))
#
# The 'seen' deque holds the last 'n' seen values, where seen[-1] is the
# most recently seen, therefore letting j = 0 gives the equation for the
# next predicted value.
next_val = seen[-Params.n + Params.m] ^ timesA(
upper(seen[-Params.n]) | lower(seen[-Params.n + 1]))
seen.append(next_val)
predicted = temper(next_val)
actual = sys.stdin.readline()
if not actual:
print('end of input -- {} predicted correctly, {} failures'.format(
num_correct, num_incorrect))
sys.exit(0)
actual = int(actual)
if predicted == actual:
status = 'CORRECT'
num_correct += 1
else:
status = 'FAIL'
num_incorrect += 1
print('predicted {} got {} -- {}'.format(predicted, actual, status))
- 코드 분석
from __future__ import print_function
import sys
import collections # deque 사용을 위한 모듈
__future__ 은 python2와 python3의 호환성을 위한 것으로서 python3를 사용한다면 사실상 필요 없는 코드이다.
collections는 이후 seen 변수로 deque를 사용할 때 필요한 모듈
class Params:
# clearly a mathematician and not a programmer came up with these names
# because a dozen single-letter names would ordinarily be insane
w = 32 # word size
n = 624 # degree of recursion
m = 397 # middle term
r = 31 # separation point of one word
a = 0x9908b0df # bottom row of matrix A
u = 11 # tempering shift
s = 7 # tempering shift
t = 15 # tempering shift
l = 18 # tempering shift
b = 0x9d2c5680 # tempering mask
c = 0xefc60000 # tempering mask
주석 속 여담으로 이렇게 한 글자로 모든 변수를 생성한 것은 미친 짓이기 때문에 프로그래머가 아닌 수학자가 이렇게 명명했다고 한다...
무튼 w는 32비트를 칭하는 것으로 단어 길이를 뜻하고, n(624)는 내부 상태 배열의 크기, m은 상태 배열을 섞을 때 사용하는 offset 값, r(31)은 이후 32bit를 31/1로 분리하기 위해 사용하는 변수이다.
a, b, c는 난수 변환 시 사용되는 16진수 마스크값이다.
def undo_xor_rshift(x, shift):
''' reverses the operation x ^= (x >> shift) '''
result = x
for shift_amount in range(shift, Params.w, shift):
result ^= (x >> shift_amount)
return result
undo_xor_rshift() 함수는 여러 번의 XOR을 통해 원래 값으로 복원하는 함수이다.
즉 temper 함수에서 x ^= (x >> shift) 했던 연산을 다시 for 루프로 복원하는 작업
def undo_xor_lshiftmask(x, shift, mask):
''' reverses the operation x ^= ((x << shift) & mask) '''
window = (1 << shift) - 1
for _ in range(Params.w // shift):
x ^= (((window & x) << shift) & mask)
window <<= shift
return x
undo_xor_lshiftmask() 함수는 왼쪽 shift와 mask 연산을 통해 원래 값으로 복원하는 함수
즉 temper 함수에서 x ^= ((x << shift) & mask) 했던 연산을 다시 복원하는 작업이다.
def temper(x):
''' tempers the value to improve k-distribution properties '''
x ^= (x >> Params.u)
x ^= ((x << Params.s) & Params.b)
x ^= ((x << Params.t) & Params.c)
x ^= (x >> Params.l)
return x
def untemper(x):
''' reverses the tempering operation '''
x = undo_xor_rshift(x, Params.l)
x = undo_xor_lshiftmask(x, Params.t, Params.c)
x = undo_xor_lshiftmask(x, Params.s, Params.b)
x = undo_xor_rshift(x, Params.u)
return x
메르센 트위스터가 temper 함수를 통해 난수를 생성하고, 이 프로그램에서는 untemper 함수를 통해 메르센 트위스터의 내부 상태를 추정할 수 있다.
temper 함수는 메르센이 생성한 난수를 통계적으로 더 무작위하게 만드는 단계이며, untemper는 temper 과정에서 변형된 난수를 원래 상태로 복원한다.
def upper(x): # 32-31=1이므로 상위 1비트 반환
''' return the upper (w - r) bits of x '''
return x & ((1 << Params.w) - (1 << Params.r))
def lower(x): # 하위 31비트 반환
''' return the lower r bits of x '''
return x & ((1 << Params.r) - 1)
def timesA(x):
''' performs the equivalent of x*A '''
if x & 1: # x의 최하위 비트가 1
return (x >> 1) ^ Params.a
else: # x의 최하위 비트가 0
return (x >> 1)
upper() 함수는 숫자 x의 상위 (w-r) 비트를 반환하는데, 여기서는 32-31=1 이므로 상위 1비트를 반환한다.
lower() 함수는 숫자 x의 하위 r비트(31bit)를 반환한다.
timesA() 함수는 메르센 트위스터 알고리즘의 핵심 변환 중 하나를 수행한다.
숫자 x의 최하위 비트가 1이면, x를 오른쪽으로 1비트 shift 한 후 Params.a 와 XOR 한다.
최하위 비트가 0이면, 그냥 1비트 시프트만 진행한다.
seen = collections.deque(maxlen=Params.n)
print('waiting for {} previous inputs'.format(Params.n))
for _ in range(Params.n):
val = untemper(int(sys.stdin.readline()))
seen.append(val)
seen은 마지막으로 본 624개의 값을 저장하는 데에 사용되는 큐(deque)이다.
이 큐는 최대 길이가 Params.a(624)이며, 새 값이 추가될 경우 가장 오래된 값이 자동으로 제거된다.
여기의 for 루프 부분이 바로 624개의 초기값을 입력으로 받는 부분이며 sys.stdin.readline()으로 입력받는다.
untemper 함수를 사용해 이 값을 원래 내부 상태로 복원한 후, seen 큐에 추가한다.
num_correct = num_incorrect = 0 # 정확히 & 잘못 예측한 횟수를 각각 초기화
print('ready to predict') # 예측 시작 준비 완료
while True:
# The recurrence relation is:
#
# x[k + n] = x[k + m] ^ timesA(upper(x[k]) | lower(x[k + 1]))
#
# Substituting j = k + n gives
#
# x[j] = x[j - n + m] ^ timesA(upper(x[j - n]) | lower(x[j - n + 1]))
#
# The 'seen' deque holds the last 'n' seen values, where seen[-1] is the
# most recently seen, therefore letting j = 0 gives the equation for the
# next predicted value.
next_val = seen[-Params.n + Params.m] ^ timesA(
upper(seen[-Params.n]) | lower(seen[-Params.n + 1]))
seen.append(next_val)
predicted = temper(next_val)
actual = sys.stdin.readline()
if not actual:
print('end of input -- {} predicted correctly, {} failures'.format(
num_correct, num_incorrect))
sys.exit(0)
actual = int(actual)
if predicted == actual:
status = 'CORRECT'
num_correct += 1
else:
status = 'FAIL'
num_incorrect += 1
print('predicted {} got {} -- {}'.format(predicted, actual, status))
- 핵심 연산 => x[j] = x[j - n + m] ^ timesA(upper(x[j - n]) | lower(x[j - n + 1]))
while 루프를 통해 종료 신호를 받을 때까지 계속 예측을 시도한다.
다음 값을 예측하기 위해 내부 상태(seen)에서 필요한 두 값을 XOR 연산으로 계산한다.
여기서 predicted는 예측된 값을 의미하고, 실제 입력된 값인 actual 과 비교하여 예측 정답 유무를 판단한다!
이제 예시를 통해 비트 연산이 수행되는 과정을 더 자세히 살펴보자.
총 624개의 숫자가 입력되어야 하지만... 일단 숫자 하나만 입력되는 경우를 예로 들어보도록 하겠다.
입력값 : 3499211612
2진수 표현: 11010 00010 11011 10100 01110 10111 00 (32 bit)
이 숫자가 입력되면 val = untemper(3499211612)을 통해 untemper 함수로 넘어가게 된다.
untemper 함수는 아래 temper 함수에서 수행된 비트 연산 단계를 역으로 수행한다.
<temper 함수의 연산 단계>
- x ^= (x >> Params.u)
- x ^= ((x << Params.s) & Params.b)
- x ^= ((x << Params.t) & Params.c)
- x ^= (x >> Params.l)
<untemper 함수의 연산 단계>
- x = undo_xor_rshift (x, Params.l)
- x = undo_xor_lshiftmask (x, Params.t, Params.c)
- x = undo_xor_lshiftmask (x, Params.s, Params.b)
- x = undo_xor_rshift (x, Params.u)
1. undo_xor_rshift(x, Params.l)
def undo_xor_rshift(x, shift):
''' reverses the operation x ^= (x >> shift) '''
result = x
for shift_amount in range(shift, Params.w, shift):
result ^= (x >> shift_amount)
return result
untemper 함수는 먼저 앞서 temper 함수의 마지막 단계였던 x ^= (x >> Params.l) 연산을 먼저 역으로 수행한다.
Params.l = 18이므로
shift = 18
x = 3499211612 = 11010 00010 11011 10100 01110 10111 00
<1차 오른쪽 shift : x >> 18 >
shifted = 00000 00000 00000 00011 01000 01011 01
<XOR 수행>
result = 11010 00010 11011 10100 01110 10111 00 (원래 값)
result ^= 00000 00000 00000 00011 01000 01011 01 (shifted 값)
result = 11010 00010 11011 10111 00110 11100 01
2. undo_xor_lshiftmask (x, Params.t, Params.c)
def undo_xor_lshiftmask(x, shift, mask):
''' reverses the operation x ^= ((x << shift) & mask) '''
window = (1 << shift) - 1
for _ in range(Params.w // shift):
x ^= (((window & x) << shift) & mask)
window <<= shift
return x
다음으로 x ^= ((x << Params.t) & Params.c) 연산을 역으로 수행한다.
현재 Params.t = 15 이며 Params.c = 0xefc60000 이다.
shift = 15
mask = 0xefc60000 = 11101 11111 00011 00000 00000 00000 00
<1차 왼쪽 shift : x << 15>
shifted = 11010 00010 11011 10111 00110 11100 01000 00000 00000 000
<마스크 적용>
masked = shifted & mask = 11000 00000 00000 00000 00000 00000 00
<XOR 수행>
result ^= masked
result = 11010 00010 11011 10111 00110 11100 01 (현재 값)
result ^= 11000 00000 00000 00000 00000 00000 00
result = 00010 00010 11011 10111 00110 11100 01
3. undo_xor_lshiftmask (x, Params.s, Params.b)
다음으로 x ^= ((x << Params.s) & Params.b) 연산을 역으로 수행한다.
현재 Params.s = 7 이며 Params.b = 0x9d2c5680 이다.
shift = 7
mask = 0x9d2c5680 = 10011 10100 10110 00101 01101 00000 00
<1차 왼쪽 shift : x << 7>
shifted = 00000 01011 01110 11100 11011 10001 00000 00000 0000
<마스크 적용>
masked = shifted & mask = 00000 00000 00110 00100 00000 00000 00
<XOR 수행>
result ^= masked
result = 00010 00010 11011 10111 00110 11100 01 (현재 값)
result ^= 00000 00000 00110 00100 00000 00000 00
result = 00010 00010 11101 10011 00110 11100 01
4. undo_xor_rshift(x, Params.u)
마지막으로 x ^= (x >> Params.u) 연산을 역으로 수행한다.
Params.u = 11이므로
shift = 11
x = 00010 00010 11101 10011 00110 11100 01 (현재 값)
<1차 오른쪽 shift : x >> 11>
shifted = 00000 00000 00000 10000 10111 01100 11
<XOR 수행>
result ^= shifted
result = 00010 00010 11101 10011 00110 11100 01 (현재 값)
result ^= 00000 00000 00000 10000 10111 01100 11
result = 00010 00010 11101 00011 10001 10000 10
따라서 이렇게 최종적으로 untemper을 통해 복구된 내부 상태는 00010000101110100011100011000010 이며, 이를 10진수로 변환하면 1234567890이다. 이것이 바로 해당 프로그램의 첫 번째 untemper 함수에서 복구된 값이 되는 것!
이렇게 복구된 첫 번째 값이 seen 큐에 추가되고, 이후 입력된 나머지 623개의 값들이 모두 동일한 방식으로 untemper 과정을 거쳐 seen 큐에 차례대로 추가된다.
이후 seen 큐가 가득 차면, while문으로 진입하여 새로운 난수를 예측하기 시작한다.
while True:
next_val = seen[-Params.n + Params.m] ^ timesA(
upper(seen[-Params.n]) | lower(seen[-Params.n + 1]))
seen.append(next_val)
predicted = temper(next_val)
actual = sys.stdin.readline()
if not actual:
print('end of input -- {} predicted correctly, {} failures'.format(
num_correct, num_incorrect))
sys.exit(0)
actual = int(actual)
if predicted == actual:
status = 'CORRECT'
num_correct += 1
else:
status = 'FAIL'
num_incorrect += 1
print('predicted {} got {} -- {}'.format(predicted, actual, status))
624개의 숫자는 너무 많으니 첫 번째 값이 1234567890, 마지막 624번째로 복구된 값이 987654321 라고 가정해보겠다.
next_val 계산
next_val = seen[-624 + 397] ^ timesA(upper(seen[-624]) | lower(seen[-623]))- seen[-624]는 가장 오래된(첫 번째) 복구된 값 : 1234567890
- seen[-623]은 두 번째 복구된 값 : 1122334455 (가정)
- seen[-227]는 중간 지점의 값 : 397번째 값인 765432100 (가정)
upper(seen[-624])
- 여기서 1234567890은 2진수로 0100 1001 1001 0110 0000 0010 1101 0010 이다.
- upper 함수는 Params.r = 31을 사용하여 상위 1비트를 가져오므로, upper(seen[-624]) = 1227133512 이다.
upper(1234567890) = 01001001100101100000001011010010 & (11111111111111111111111111111110)
= 01001001100101100000001011000000
이런 방식으로 lower 함수는 하위 31비트를 가져와서 두 값을 OR 비트 연산을 한 값을 timesA 함수에 전달한다.
timesA 함수는 입력값이 홀수인지 확인하고, 홀수 즉 최하위 비트가 1이라면 Params.a와 XOR 연산을 수행한다.
이렇게 생성된 next_val을 temper 함수를 거쳐 최종 예측값인 predicted를 생성해내는데, 이 예측값은 해당 프로그램이 다음에 생성할 난수라고 예측하는 값인 것이다.
따라서 이 예측된 값 predicted와 실제로 입력되는 값 actual을 비교하여, 예측이 맞았는지를 확인한다.
위 과정을 반복하여 프로그램은 계속해서 난수를 예측할 수 있고, 예측된 값이 실제 생성된 값과 일치하면 프로그램은 내부 상태를 올바르게 복구한 것이다.
<핵심 요약>
- 메르센 트위스터의 tempering 및 비트 조작 과정을 되돌려 내부 상태를 복구한다.
- 624개의 출력을 본 후, 이 상태를 이용해 이후의 출력을 예측할 수 있다.
- 이는 메르센 트위스터가 가진 보안적 취약성을 보여주며, 초기 시드를 알 필요 없이 충분한 출력을 관찰하면 난수를 예측할 수 있다는 것이 핵심
#include <iostream>
#include <random>
int main()
{
std::mt19937 mt{std::random_device{}()};
// optional -- advance to some arbitrary point in the sequence
mt.discard(8675309);
for(int i = 0; i < 624 + 10; i++) {
std::cout << mt() << '\n';
}
}
메르센 트위스터를 수행하는 testcase.cpp의 코드는 위와 같다.
위 코드로 624개의 testcase를 사전에 준비해놓은 상태에서 mersenne_predict.py로 다음 난수 예측을 시작한다.
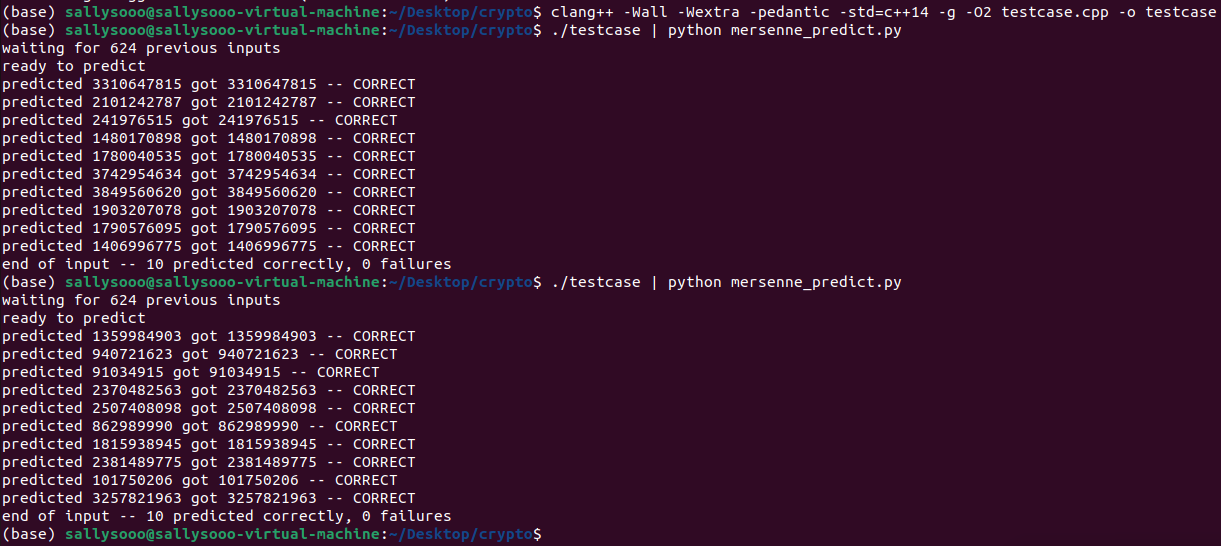
실행해보면 위와 같이 전부 correct로 뜨는 것을 볼 수 있다!
'Cryptography' 카테고리의 다른 글
| [Crypto] 암호학 기본 개념 및 SSH 이해하기 - 대칭키(AES), 비대칭키(RSA) 알고리즘 (0) | 2024.11.28 |
|---|---|
| [Crypto] Double DES 문제 풀이 (0) | 2024.08.31 |
| [Crypto] 고전 암호와 현대 암호 알아보기 (1) | 2024.08.30 |
| [Crypto] 암호학 툴 설치하기 (0) | 2024.08.27 |
| [Crypto] 난수 생성기 : 메르센 트위스터 (Mersenne Twister) 알아보기 (0) | 2024.08.25 |
