1. 큰 그림 보기
- to do : 캘리포니아 인구 조사 데이터를 사용해 캘리포니아의 주택 가격 모델 만들기
- 캘리포니아 block group 마다 population, median income, median housing price 등을 담고 있음
- block group : 미국 인구 조사국에서 샘플 데이터를 발표하는데 사용하는 최소한의 지리적 단위 (한 구역당 보통 600~3000명의 인구를 나타냄)
- 목표 : 해당 데이터로 모델을 학습시켜 다른 측정 데이터가 주어졌을 때 구역의 중간 주택 가격을 예측
1.1 문제 정의

Q1. 비즈니스의 목적이 정확히 무엇인가?
A. 이 모델의 출력이 여러 가지 다른 신호(정보)와 함께 다른 머신러닝 시스템에 입력으로 사용됨
* pipeline : 데이터 처리 component 들이 연속되어 있는 것
- 머신러닝 시스템은 데이터를 조작하고 변환할 일이 많아 파이프라인을 사용하는 일이 매우 흔함
- 컴포넌트들은 비동기적으로 작동하며, 완전히 독립적으로 컴포넌트 사이의 인터페이스는 데이터 저장소 뿐!
Q2. 현재 솔루션의 구성?
A. 현재는 구역 주택 가격을 전문가가 수동으로 추정함 & 구역의 데이터를 기반으로 중간 주택 가격을 예측하는 모델을 훈련시키는 쪽이 유용하다고 판단
Q3. 모델 선정?
- label된 훈련 sample이 있다. => 지도 학습
- 모델이 값을 "예측"해야한다. => 회귀 문제
- 예측에 사용할 특성이 "여러 개"(구역의 인구, 중간 소득 등)이다. => 다중 회귀(multiple regression)
- 각 구역마다 "하나의 값"을 예측한다. => 단변량 회귀(unvariable regression)
- 이 시스템으로 들어오는 데이터에 연속적인 흐름이 없으므로 빠르게 변하는 데이터에 적응하지 않아도 되며, 데이터가 메모리에 들어갈 만큼 충분히 작음 => 일반적인 배치 학습
1.2 성능 측정 지표 선택
- 회귀 문제의 전형적인 성능 지표는 평균 제곱근 오차(RMSE)
=> 오차가 커질수록 이 값은 더욱 커지므로 예측에 얼마나 많은 오차가 있는지 가늠하게 해줌

- RMSE는 일반적으로 회귀 문제에서 선호되는 성능 측정 방법이지만, 경우에 따라 다른 함수를 사용할 수도 있음
=> 이상치로 보이는 구역이 많다면 평균 절대 오차(MAE) 고려 가능!

- RMSE와 MAE 모두 예측값의 벡터와 target 값의 벡터 사이의 거리를 재는 방법!
- 거리 측정에는 여러 가지 방법(or 'norm')을 사용할 수 있음
ex) 유클리드 노름, 맨해튼 노름 등
- 노름의 지수가 클수록 큰 값의 원소에 치우치며 작은 값은 무시된다.
- 그래서 RMSE가 MAE보다 조금 더 이상치에 민감함
- 그러나 이상치가 매우 드물면 RMSE가 잘 맞기 때문에 일반적으로 널리 사용됨
1.3 가정 검사
2. 데이터 가져오기
예시 코드 및 코랩 자료 링크
https://github.com/rickiepark/handson-ml3
http://bit.ly/3K5sOoj
from pathlib import Path
import pandas as pd
import tarfile
import urllib.request
def load_housing_data():
tarball_path = Path("datasets/housing.tgz")
if not tarball_path.is_file():
Path("datasets").mkdir(parents=True, exist_ok=True)
url = "https://github.com/ageron/data/raw/main/housing.tgz"
urllib.request.urlretrieve(url, tarball_path)
with tarfile.open(tarball_path) as housing_tarball:
housing_tarball.extractall(path="datasets")
return pd.read_csv(Path("datasets/housing/housing.csv"))
housing = load_housing_data()
위 함수를 호출하면 datasets/housing.tgz 파일을 찾게 되는데, 이를 찾지 못하면 현재 디렉터리(기본: /content 내부) 안에 datasets 디렉터리를 만들고, ageron/data 깃허브 저장소에서 housing.tgz 파일을 다운로드하여 /content 디렉터리에 압축을 푼다.
이렇게 하면 datasets/housing 디렉터리가 생성되며 그 안에 housing.csv 파일이 있게된다!
마지막으로 해당 csv 파일에 있는 모든 데이터를 판다스 데이터프레임으로 로드하고 이 객체를 반환한다.


- total_bedrooms 특성은 20,443개만 널값이 아니라는 점에 주목해야 함
=> 207개의 구역이 해당 특성을 갖고 있지 않다는 의미!
- ocean_proximity 필드만 빼고 모든 특성이 숫자형 => categorical value


- std: 값이 퍼져 있는 정도를 측정하는 표준 편차를 나타냄
- 25%, 50%, 75% 행은 백분위수(percentile)를 나타냄 => 전체 관측값에서 주어진 백분율이 속하는 하위 부분의 값
import matplotlib.pyplot as plt
# 추가 코드 – 다음 다섯 라인은 기본 폰트 크기를 지정합니다
plt.rc('font', size=14)
plt.rc('axes', labelsize=14, titlesize=14)
plt.rc('legend', fontsize=14)
plt.rc('xtick', labelsize=10)
plt.rc('ytick', labelsize=10)
housing.hist(bins=50, figsize=(12, 8))
save_fig("attribute_histogram_plots") # 추가 코드
plt.show()
위 히스토그램으로부터 다음 사항들을 확인할 수 있다.
1. median_income 특성이 US 달러로 표현되어 있지 않음
스케일을 조정하고 상한이 15, 하한이 0.5가 되도록 만들었기에, 중간 소득 특성은 대략 수만 달러를 나타냄
2. housing_median_age와 median_house_value 역시 최댓값과 최솟값을 한정함
후자의 중간 주택 가격의 경우는 타깃 속성(label)로 사용되기 때문에 심각한 문제가 될 수 있음
=> 가격이 한곗값을 넘어가지 않도록 머신러닝 알고리즘이 학습될지도 모른다.
3. 특성들의 스케일이 서로 많이 다르다.
4. 마지막으로 많은 히스토그램에서 오른쪽 꼬리가 더 길다.
이러한 형태는 일부 머신러닝 알고리즘에서 패턴을 찾기 어렵게 만듦
<테스트 세트 만들기>
데이터 스누핑(data snooping) 편향을 방지하기 위해 테스트 세트를 따로 떼놓아야 한다.
import numpy as np
def shuffle_and_split_data(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = shuffle_and_split_data(housing, 0.2)

Q. 계층적 샘플링?
- 예를 들어 미국인 1000명에게 설문조사를 할 때 미국 인구의 51.1%가 여성이고 48.9%가 남성이라면, 잘 구성된 설문조사는 샘플에서도 이 비율을 유지하여 여성 511명, 남성 489명으로 설정해야한다.
- 전체 인구는 '계층'이라는 동질의 그룹으로 나뉘고, 테스트 세트가 전체 인구를 대표하도록 각 계층에서 올바른 수의 샘플을 추출
- 계층별로 데이터셋에 충분한 샘플 수가 있어야 함
=> 안그러면 계층의 중요도를 추정하는데 편향이 발생할 것!
=> 즉, 너무 많은 계층으로 나누어서는 안 되며 각 계층이 충분히 커야 한다는 뜻
# 추가 코드 – 나쁜 샘플을 얻을 확률 10.7%를 계산하는 방법
from scipy.stats import binom
sample_size = 1000
ratio_female = 0.511
proba_too_small = binom(sample_size, ratio_female).cdf(485 - 1)
proba_too_large = 1 - binom(sample_size, ratio_female).cdf(535)
print(proba_too_small + proba_too_large)
인구의 여성 비율이 51.1%일 때 1,000명으로 구성된 랜덤 샘플에서 여성이 48.5% 보다 작거나 53.3% 보다 많을 확률을 계산하려면 이항 분포를 사용한다.
이항 분포의 'cdf()' 메서드는 여성의 수가 주어진 값보다 작거나 같을 확률을 반환한다.
housing["income_cat"] = pd.cut(housing["median_income"],
bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
labels=[1, 2, 3, 4, 5])
위 코드는 pd.cut() 함수를 사용해서 카테고리 5개를 가진 소득 카테고리 특성을 만든 것이다.
=> 카테고리 1은 0~1.5까지 범위이고, 카테고리 2는 1.5~3까지 범위가 되는 식

이제 소득 카테고리를 기반으로 계층적 샘플링을 수행할 준비를 마쳤다.
사이킷런은 sklearn.model_selection 패키지 안에 여러 가지 분할기(splitter) 클래스를 제공함
=> 분할기 : 데이터셋을 train / test 세트로 분할하는 다양한 전략을 구현한 것으로, 모두 split() 메소드를 보유
split() 메소드를 train과 test 데이터 자체가 아닌, "인덱스"를 반환한다.
교차 검증처럼 여러 개로 분할하면 모델의 성능을 더 잘 추정할 수 있다.
from sklearn.model_selection import StratifiedShuffleSplit
splitter = StratifiedShuffleSplit(n_splits=10, test_size=0.2, random_state=42)
strat_splits = []
for train_index, test_index in splitter.split(housing, housing["income_cat"]):
strat_train_set_n = housing.iloc[train_index]
strat_test_set_n = housing.iloc[test_index]
strat_splits.append([strat_train_set_n, strat_test_set_n])
strat_train_set, strat_test_set = strat_splits[0] # 첫 번째 분할은 이렇게 사용
위 코드는 한 데이터셋으로 각각 다른 10개의 계층 분할을 생성한 것!
계층적 샘플링은 자주 사용되기 때문에, 하나의 분할이 필요한 경우 train_test_split() 함수와 stratify 매개변수를 사용하여 다음과 같이 간편하게 만들 수 있음
strat_train_set, strat_test_set = train_test_split(
housing, test_size=0.2, stratify=housing["income_cat"], random_state=42)

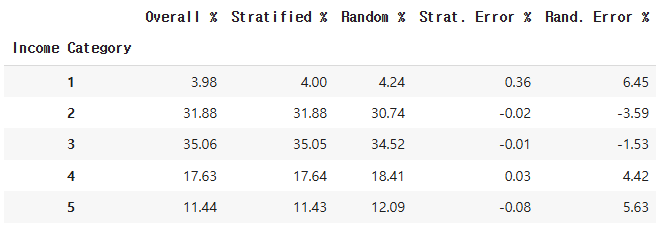
위 표는 계층 샘플링으로 만든 테스트 세트에서 소득 카테고리 비율을 비교한 것이다.
계층 샘플링을 사용해 만든 테스트 세트는 전체 데이터셋에 있는 소득 카테고리의 비율과 거의 같지만, 반면 일반 랜덤 샘플링으로 만든 테스트 세트는 비율이 많이 달라진 것을 볼 수 있다.
<데이터 시각화>


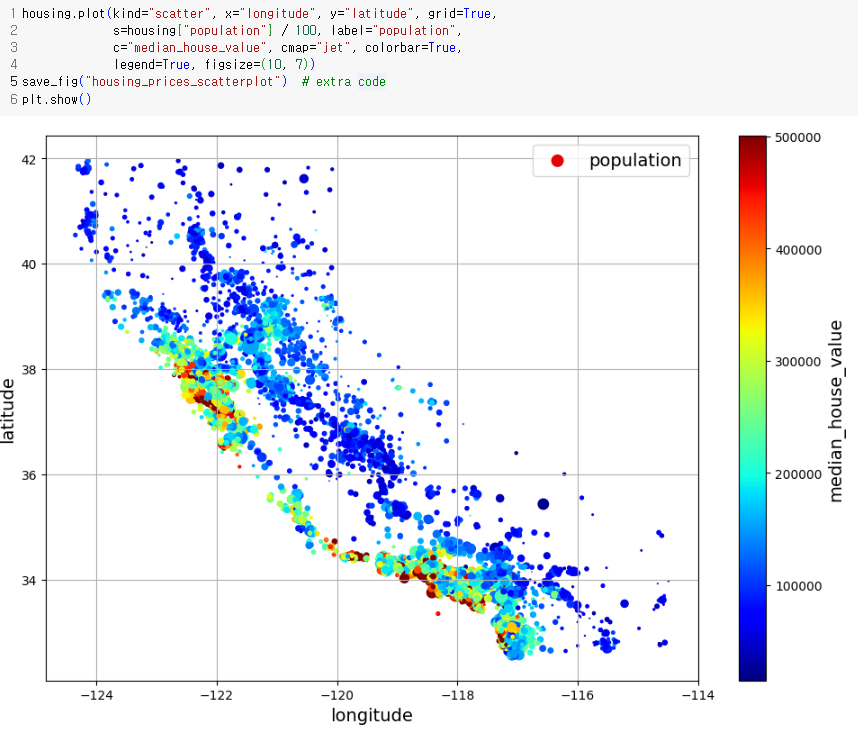
주택 가격은 확실히 바다와 인접한 곳과 같은 지역과 인구 밀도와 관련성이 높다는 것을 알 수 있다.
군집 알고리즘을 사용해 주요 군집을 찾고 군집의 중심까지의 거리를 재는 특성을 추가할 수 있다.
# 추가 코드
# 캘리포니아 이미지를 다운로드
filename = "california.png"
if not (IMAGES_PATH / filename).is_file():
homl3_root = "https://github.com/ageron/handson-ml3/raw/main/"
url = homl3_root + "images/end_to_end_project/" + filename
print("Downloading", filename)
urllib.request.urlretrieve(url, IMAGES_PATH / filename)
housing_renamed = housing.rename(columns={
"latitude": "Latitude", "longitude": "Longitude",
"population": "Population",
"median_house_value": "Median house value (ᴜsᴅ)"})
housing_renamed.plot(
kind="scatter", x="Longitude", y="Latitude",
s=housing_renamed["Population"] / 100, label="Population",
c="Median house value (ᴜsᴅ)", cmap="jet", colorbar=True,
legend=True, figsize=(10, 7))
california_img = plt.imread(IMAGES_PATH / filename)
axis = -124.55, -113.95, 32.45, 42.05
plt.axis(axis)
plt.imshow(california_img, extent=axis)
save_fig("california_housing_prices_plot")
plt.show()
또한 데이터셋이 너무 크지 않으므로 모든 특성 간의 표준 상관계수(피어슨 상관계수 r)을 corr() 메소드를 이용해 아래와 같이 쉽게 계산 가능하다.

from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms",
"housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))
save_fig("scatter_matrix_plot") # 추가 코드
plt.show()
위 산점도 행렬을 보았을때, 중간 주택 가격(median_house_value)을 예측하는 데 중간 소득(median_income)이 가장 유용해 보이기에 해당 산점도를 확대해보았다.

1. 상관관계가 매우 강하다.
2. 앞서 본 가격의 한곗값이 500,000 달러에서 수평선으로 잘 보인다.
여기 말고도 450,000 달러 근처, 350,000달러 근처에서도 잘 보이기 때문에 해당 구역을 제거할 수 있음

새로운 bedrooms_ratio 특성은 전체 방 개수나 침실 개수보다 중간 주택 가격과의 상관관계가 훨씬 높다는 것을 알 수 있음
'Ai' 카테고리의 다른 글
| [Ai] 머신러닝 시스템의 종류 및 주요 알고리즘 개념 정리 (0) | 2025.03.13 |
|---|---|
| [Ai] KNIME 사용법 및 각종 노드 활용 방법 모음 (0) | 2025.01.16 |
